 |
 |
 |
 |
 |
 |
Πώς συγκρίνουμε κλάσματα ;
Τα κλάσματα που έχουν τον ίδιο παρονομαστή, λέγονται ομώνυμα.
Τα κλάσματα που έχουν διαφορετικούς παρονομαστές λέγονται ετερώνυμα.
Για να συγκρίνουμε δύο ή περισσότερα κλάσματα, αυτά πρέπει να είναι ομώνυμα.
Π.χ. \(\frac{3}{4} > \frac{1}{4}\) .
Πράγματι : το πρώτο κλάσμα δείχνει ότι χωρίσαμε την ακέραια μονάδα σε τέσσερα ίσα μέρη και πήραμε τα τρία. Το δεύτερο κλάσμα δείχνει ότι χωρίσαμε την ακέραια μονάδα σε τέσσερα ίσα μέρη και πήραμε το ένα.
Από εδώ λοιπόν φαίνεται ότι : Ανάμεσα σε δύο ή περισσότερα ομώνυμα κλάσματα μεγαλύτερο είναι αυτό που έχει τον μεγαλύτερο αριθμητή.
Όταν έχουμε ετερώνυμα κλάσματα δεν μπορούμε να τα συγκρίνουμε, παρά μόνο, αν τα μετατρέψουμε σε δεκαδικούς ή σε ομώνυμα κλάσματα.
Ετερώνυμα που μπορούμε να συγκρίνουμε
Λίγες είναι οι περιπτώσεις στις οποίες μπορούμε να συγκρίνουμε ετερώνυμα κλάσματα :
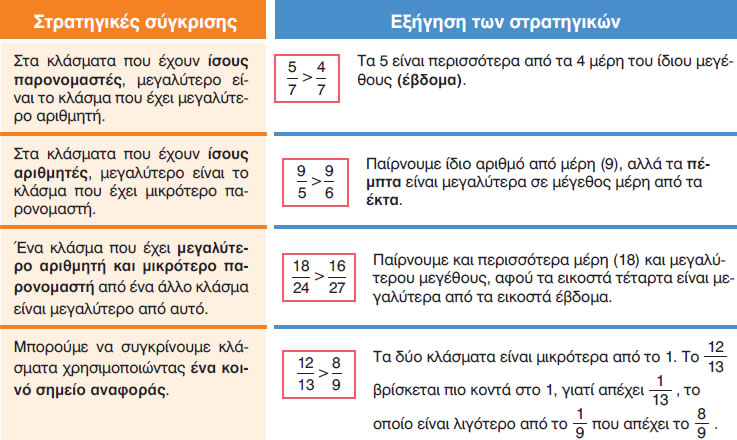
Π.χ. από τα κλάσματα \(\frac{3}{5}\) και \(\frac{3}{8}\) μεγαλύτερο είναι το πρώτο, επειδή αν χωρίσουμε μια ακέραια μονάδα (π.χ. μια πίτσα) σε 5 ίσα μέρη και μια άλλη ακέραια μονάδα (μια άλλη ίδια πίτσα) σε 8 ίσα μέρη, προφανώς μεγαλύτερα κομμάτια θα πάρουμε από την πρώτη. Άρα \(\frac{3}{5}>\frac{3}{8}\) .
Ανάμεσα σε δύο ή περισσότερα ετερώνυμα κλάσματα με τον ίδιο αριθμητή, μεγαλύτερο είναι αυτό που έχει τον μικρότερο παρονομαστή.
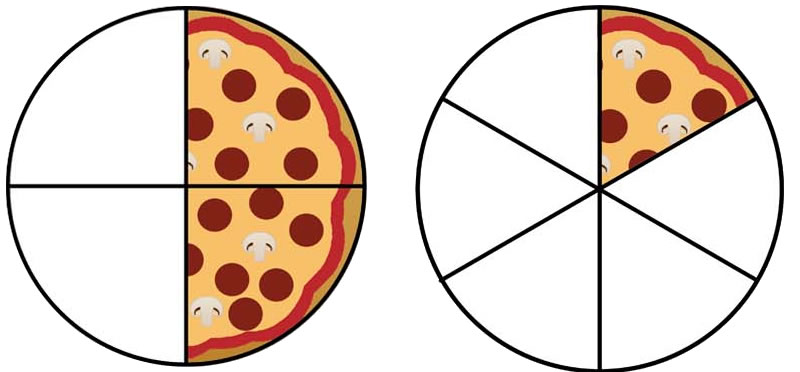
Αν έχω τα κλάσματα \(\frac{2}{4}\) και \(\frac{1}{6}\), παρατηρώ ότι το πρώτο κλάσμα χωρίζει το ολόκληρο σε λιγότερα μέρη (κι επομένως μεγαλύτερα) και παίρνει περισσότερα από αυτά τα μεγαλύτερα μέρη. Άρα \(\frac{2}{4}>\frac{1}{6}\) .
Ανάμεσα σε δύο ετερώνυμα κλάσματα μεγαλύτερο είναι εκείνο που έχει ταυτόχρονα και τον μεγαλύτερο αριθμητή και τον μικρότερο παρονομαστή.
Κλάσματα κοντά στο μισό ή το ολόκληρο
Αν έχω τα κλάσματα \(\frac{3}{5}\) και \(\frac{2}{4}\), παρατηρώ ότι και τα δύο δείχνουν μια αξία κοντά στο μισό. Αν παρατηρήσω όμως πιο προσεκτικά θα δω ότι το πρώτο κλάσμα έχει αξία μεγαλύτερη από το μισό ενώ το δεύτερο έχει αξία ακριβώς ίση με το μισό. Άρα το πρώτο είναι μεγαλύτερο και γράφουμε \(\frac{3}{5}>\frac{2}{4}\) .
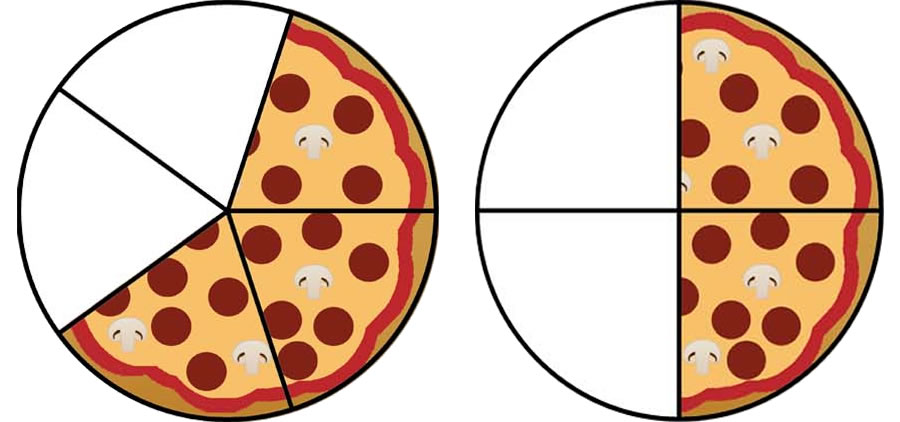
Μπορούμε, επομένως, να συγκρίνουμε δυο κλάσματα χρησιμοποιώντας ένα κοινό σημείο αναφοράς π.χ το μισό της ακέραιας μονάδας, πιο κοντά στο 0 ή πιο κοντά στο 1.
 |
 |
