03.18 Πρόσθεση και αφαίρεση κλασμάτων (21/11/2024)

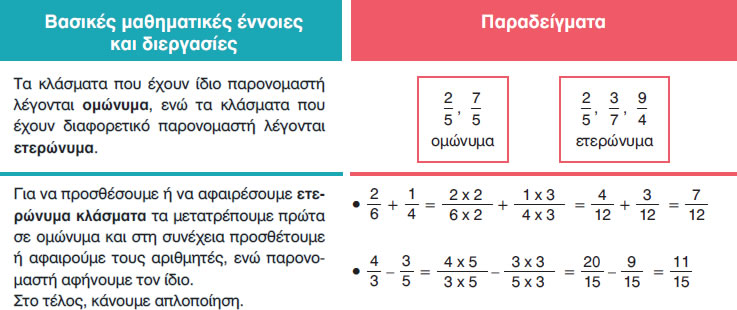
Τα κλάσματα που έχουν τον ίδιο παρονομαστή, λέγονται ομώνυμα.π.χ. \(\frac{3}{5}\) , \(\frac{4}{5}\) , \(\frac{13}{5}\) , \(\frac{9}{5}\)

Τα κλάσματα που έχουν διαφορετικούς παρονομαστές λέγονται ετερώνυμα.π.χ. \(\frac{3}{5}\) , \(\frac{4}{7}\) , \(\frac{13}{15}\) , \(\frac{9}{24}\)

Α΄ τρόπος 

Για να βρούμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών :

• Βρίσκουμε τα πολλαπλάσιά τους.
• Σημειώνουμε τα κοινά πολλαπλάσιά τους.
• Το μικρότερο από αυτά είναι το Ε.Κ.Π. των αριθμών αυτών.

Π.χ. Να βρούμε το Ε.Κ.Π. των αριθμών 12, 16

Βρίσκουμε τα πολλαπλάσια του 12 : Π₁₂ = {0, 12, 24, 36, 48, 60, 72, 84, 96, 108, ...}

Βρίσκουμε τα πολλαπλάσια του 16 : Π₁₆ = {0, 16, 32, 48, 64, 80, 96, 112, 128,...}

Παρατηρούμε ότι οι αριθμοί 48 και 96 είναι Κοινά Πολλαπλάσια. Άρα το 48 που είναι το μικρότερο από τα Κοινά Πολλαπλάσια, είναι το Ε.Κ.Π. των αριθμών 12 και 16 και γράφουμε : Ε.Κ.Π. (12, 16) = 48

Β΄ τρόπος

Για να βρούμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών :

• Εξετάζουμε αν ο μεγαλύτερος από τους αριθμούς διαιρείται (ακριβώς) από τους άλλους. Αν διαιρείται, τότε αυτός είναι το Ε.Κ.Π.
• Αν δε δαιρείται απ' όλους τότε τον, διπλασιάζουμε. Αν διαιρείται, τότε αυτός είναι το Ε.Κ.Π.
• Αν δε διαρείται απ' όλους τότε τον τριπλασιάζουμε τετραπλασιάζουμε κ.λπ.

Π.χ. Να βρεθεί το Ε.Κ.Π. των αριθμών 8, 12, 16

Μεγαλύτερος είναι το 16. Παρατηρούμε ότι δε διαιρείται από τους άλλους δύο. Τον διπλασιάζουμε και εξετάζουμε αν διαιρείται. Δε διαιρείται και από τους δύο και γι' αυτό τον τριπλασιάζουμε. Παρατηρούμε ότι αν τον τριπλασιάσουμε διαιρείται από τους άλλους δύο : 3 Χ 16 = 48 Το 48 διαιρείται ακριβώς και από το 8 και από το 12, άρα αυτό είναι το Ε.Κ.Π. Γράφουμε τότε Ε.Κ.Π. (8, 12, 16) = 48

Για να προσθέσουμε ομώνυμα κλάσματα, προσθέτουμε τους αριθμητές και το άθροισμά τους το βάζουμε αριθμητή, ενώ παρονομαστή αφήνουμε τον ίδιο.

π.χ. \(\frac{3}{9}\) + \(\frac{4}{9}\) = \(\frac{3+4}{9}\) = \(\frac{7}{9}\)

\(\frac{1}{12}\) + \(\frac{4}{12}\) + \(\frac{2}{12}\) = \(\frac{1+4+2}{9}\) = \(\frac{7}{12}\)

Για να αφαιρέσουμε ομώνυμα κλάσματα, αφαιρούμε τους αριθμητές και τη διαφορά τους τη βάζουμε αριθμητή, ενώ παρονομαστή αφήνουμε τον ίδιο.

π.χ. \(\frac{8}{9}\) - \(\frac{4}{9}\) = \(\frac{8-4}{9}\) = \(\frac{4}{9}\)

\(\frac{11}{12}\) - \(\frac{4}{12}\) - \(\frac{2}{12}\) = \(\frac{11-4-2}{9}\) = \(\frac{5}{12}\)

Για να προσθέσουμε ετερώνυμα κλάσματα, θα πρέπει να τα μετατρέψουμε πρωτα σε ομώνυμα. Ο πιο απλός τρόπος να μετατρέψουμε δυο ετερώνυμα κλάσματα σε ομώνυμα είναι να πολλαπλασιάσουμε τους όρους του καθενός με τον παρονομαστή του άλλου.

π.χ. \(\frac{3}{5}\) + \(\frac{4}{7}\) = \(\frac{3×7}{5×7}\) + \(\frac{4×5}{7×5}\) =  \(\frac{21}{35}\) + \(\frac{20}{35}\) = \(\frac{41}{35}\)

\(\frac{7}{9}\) + \(\frac{1}{2}\) = \(\frac{7×2}{9×2}\) + \(\frac{1×9}{2×9}\) =  \(\frac{14}{18}\) + \(\frac{9}{18}\) = \(\frac{23}{18}\)

Ένας άλλος τρόπος είναι να βρούμε το Ε.Κ.Π. των παρονομαστών, να διαιρέσουμε το Ε.Κ.Π. με κάθε παρονομαστή και με το πηλίκο να πολλαπλασιάσουμε τους όρους του αντίστοιχου κλάσματος.

\(\frac{3}{5}\) + \(\frac{2}{3}\) + \(\frac{5}{6}\) Ε.Κ.Π._{5, 3, 6} : 30

\(\frac{3×6}{5×6}\) + \(\frac{2×10}{3×10}\) + \(\frac{5×5}{6×5}\) = \(\frac{18}{30}\) + \(\frac{20}{30}\) + \(\frac{25}{30}\) = \(\frac{63}{30}\) = 2 \(\frac{3}{30}\) = 2\(\frac{1}{10}\)

Για να αφαιρέσουμε ετερώνυμα κλάσματα πρέπει να τα μετατρέψουμε πρώτα σε ομώνυμα πολλαπλασιάζοντας τους όρους του καθενός με τον παρονομαστή του άλλου.

π.χ. \(\frac{4}{5}\) - \(\frac{2}{7}\) = \(\frac{4×7}{5×7}\) - \(\frac{2×5}{7×5}\) =  \(\frac{28}{35}\) - \(\frac{10}{35}\) = \(\frac{18}{35}\)

\(\frac{5}{6}\) - \(\frac{2}{3}\) = \(\frac{5×3}{6×3}\) - \(\frac{2×6}{3×6}\) =  \(\frac{15}{18}\) - \(\frac{12}{18}\) = \(\frac{3}{18}\) = \(\frac{1}{6}\)

Άλλος τρόπος είναι να βρούμε το Ε.Κ.Π. των παρονομαστών και μετά να πολλαπλασιάσουμε τους όρους του κάθε κλάσματος με το πηλίκο του Ε.Κ.Π. με τον παρονομαστή του.

\(\frac{3}{4}\) - \(\frac{2}{6}\)  Ε.Κ.Π. _{4, 6} : 12

\(\frac{3}{4}\) - \(\frac{2}{6}\) = \(\frac{3×3}{4×3 }\) - \(\frac{2×2 }{6×2}\) = \(\frac{9}{12  }\) - \(\frac{4  }{12}\) = \(\frac{5  }{12}\)     

Για να προσθέσουμε ή να αφαιρέσουμε μεικτούς αριθμούς :

Μετατρέπουμε τους μεικτούς σε κλάσματα και κάνουμε την πρόσθεση ή την αφαίρεση όπως είπαμε παραπάνω.

2 \(\frac{3}{5}\) + 3 \(\frac{4}{7}\) =  \(\frac{13}{5}\) + \(\frac{25}{7}\) = \(\frac{13×7}{5×7}\) - \(\frac{25×5}{7×5}\) = \(\frac{91}{35}\) + \(\frac{125}{35}\) =\(\frac{216}{35}\) =6 \(\frac{6}{35}\)

Προσθέτουμε ή αφαιρούμε χωριστά τα ακέραια και τα κλασματικά μέρη και μετά τα προσθέτουμε

3 \(\frac{6}{7}\) - 1\(\frac{4}{5}\) = 2 + (\(\frac{6×5}{7×5}\) - \(\frac{4×7}{5×7}\))  = 2 + (\(\frac{30}{35}\) - \(\frac{28}{35}\)) = 2\(\frac{2}{35}\)