|
|
 |
 |
 |
 |
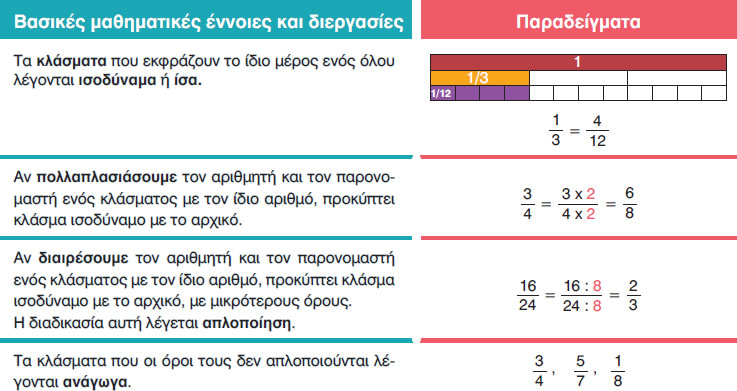
Διαφορετικά κλάσματα - ίδια αξία
Παρ' ότι έχουμε χωρίσει την κάθε πίτσα σε διαφορετικά ίσα μέρη και παρ΄ ότι κάθε φορά 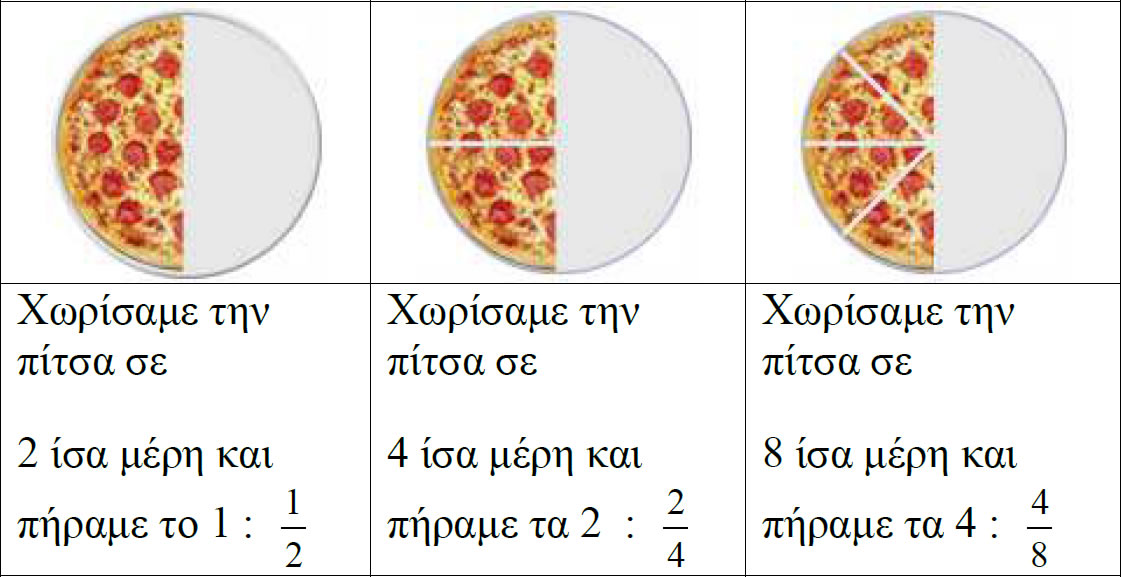 παίρναμε διαφορετικό αριθμό κομματιών, παρατηρούμε ότι και τις τρεις φορές παίρνουμε την ίδια ποσότητα. Άρα τα κλάσματα $\frac{1}{2}$ , $\frac{2}{4}$ και $\frac{4}{8}$ έχουν την ίδια αξία κι ας έχουν διαφορετικούς όρους. Γράφουμε τότε : $\frac{1}{2}$ = $\frac{2}{4}$ = $\frac{4}{8}$
παίρναμε διαφορετικό αριθμό κομματιών, παρατηρούμε ότι και τις τρεις φορές παίρνουμε την ίδια ποσότητα. Άρα τα κλάσματα $\frac{1}{2}$ , $\frac{2}{4}$ και $\frac{4}{8}$ έχουν την ίδια αξία κι ας έχουν διαφορετικούς όρους. Γράφουμε τότε : $\frac{1}{2}$ = $\frac{2}{4}$ = $\frac{4}{8}$
Άρα, υπάρχουν κλάσματα που ενώ έχουν διαφορετικούς όρους, δηλαδή διαφορετικό αριθμητή και παρονομαστή, έχουν την ίδια αξία. Αυτά τα κλάσματα λέγονται ισοδύναμα κλάσματα.
Δηλαδή το $\frac{1}{2}$ είναι ισοδύναμο με το κλάσμα $\frac{2}{4}$ και με το κλάσμα $\frac{4}{8}$ και το κάθε ένα από αυτά είναι ισοδύναμο με τα άλλα.
Ίδια αξία πολλαπλασιάζοντας
Ίδια αξία διαιρώντας
Ας παρατηρήσουμε τώρα κάτι άλλο :
$\frac{4:2}{8:2}$ = $\frac{2}{4}$ και $\frac{2:2}{4:2}$ = $\frac{1}{2}$
Αν διαιρέσουμε τους όρους ενός κλάσματος με τον ίδιο αριθμό, παίρνουμε ένα άλλο κλάσμα, που είναι ισοδύναμο με το πρώτο.
ΠΡΟΣΟΧΗ : Δεν μπορούμε να πούμε ότι τα κλάσματα $\frac{1}{2}$ , και $\frac{2}{4}$ είναι ισοδύναμα αν η μονάδα δεν είναι ίδια.
Π.χ. άλλη αξία έχει το $\frac{1}{2}$ μιας ατομικής πίτσας και άλλη το $\frac{1}{2}$ μιας οικογενειακής
Τι είναι η απλοποίηση κλάσματος ;

Πιο εύκολα καταλαβαίνουμε ή πιο εύκολα κάνουμε πράξεις με τα κλάσματα που έχουν μικρότερους όρους απ’ ό,τι με εκείνα που έχουν μεγαλύτερους.
Γι’ αυτό πολλές φορές διαιρούμε και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό, για να πάρουμε ένα κλάσμα ίσης αξίας (ισοδύναμο δηλαδή) αλλά με μικρότερους όρους, ώστε να το καταλάβουμε καλύτερα ή να κάνουμε τις πράξεις πιο εύκολα.
Αυτή η διαδικασία λέγεται απλοποίηση του κλάσματος.
Αν κάνουμε συνεχώς απλοποιήσεις σ' ένα κλάσμα ή αν διαιρέσουμε με τον Μέγιστο Κοινό Διαιρέτη του αριθμητή και του παρονομαστή, δε θα μπορούμε να συνεχίσουμε την απλοποίηση. Το κλάσμα που δεν απλοποιείται λέγεται ανάγωγο κλάσμα.
 |
 |