 |
 |
 |
 |
 |
 |
Τι είναι διαιρέτης ενός αριθμού ;
Διαιρέτης ενός αριθμού είναι κάθε αριθμός που διαιρεί τον άλλο αριθμό ακριβώς, χωρίς δηλαδή να αφήνει υπόλοιπο. Π.χ. διαιρέτης του 12 είναι το 6 επειδή διαιρεί το 12 ακριβώς.
Πότε χρειαζόμαστε τους διαιρέτες ενός αριθμού ;
Πολλές φορές χρειάζεται να εξετάσουμε με πόσους δυνατούς τρόπους μπορούμε να μοιράσουμε έναν αριθμό χωρίς να έχουμε υπόλοιπο. π.χ. Σε πόσες δυάδες, τριάδες κ.λπ. μπορούν να μοιραστούν οι μαθητές μιας τάξης.
Κάποιες άλλες φορές χρειάζεται να ξέρουμε πώς θα μοιράσουμε διάφορες ποσότητες, ώστε να δημιουργήσουμε ομοιόμορφα σύνολα. Π.χ. Πώς θα μοιράσουμε διάφορα είδη λουλουδιών, ώστε σε κάθε ανθοδέσμη να υπάρχει ο ίδιος αριθμός από κάθε είδος.
Για να λύσουμε τέτοια προβλήματα θα πρέπει να μπορούμε να βρούμε τους διαιρέτες ενός αριθμού, τους κοινούς διαιρέτες κάποιων αριθμών ή το Μέγιστο Κοινό Διαιρέτη τους (Μ.Κ.Δ.).
Ποιος αριθμός λέγεται κοινός διαιρέτης δύο ή περισσότερων αριθμών ;
Κοινός διαιρέτης δύο ή περισσότερων αριθμών είναι ο αριθμός που τους διαιρεί όλους ακριβώς.
Π.χ. ποιοι είναι οι κοινοί διαιρέτες του 12 και του 6 ;
δ12 : 1, 2, 3, 4, 6, 12 δ6 : 1, 2, 3, 6 Αριθμοί που διαιρούν και το 12 και το 6 είναι : 1, 2, 3, 6. Αυτοί οι αριθμοί είναι οι Κοινοί Διαιρέτες του 12 και του 6.
Ποιος είναι ο Μέγιστος Κοινός Διαιρέτης (Μ.Κ.Δ.) ;
Μέγιστος Κοινός Διαιρέτης δύο ή περισσότερων αριθμών είναι ο μεγαλύτερος από τους κοινούς διαιρέτες των αριθμών αυτών.
Π.χ. Στο παραπάνω παράδειγμα βρήκαμε ότι κοινοί διαιρέτες των αριθμών 12 και 6 είναι οι αριθμοί 1, 2, 3 και 6. Από αυτούς ο μεγαλύτερος, δηλαδή το 6, είναι ο Μ.Κ.Δ. του 12 και του 6.
Πώς βρίσκουμε τον Μ.Κ.Δ. ;
Α΄ τρόπος
Ο πιο απλός τρόπος για να βρούμε τον Μ.Κ.Δ. δύο ή περισσότερων αριθμών είναι :
- Να βρούμε πρώτα τους διαιρέτες τους.
- Να ξεχωρίσουμε τους κοινούς διαιρέτες.
- Να βρούμε τον μεγαλύτερο από αυτούς.
Παράδειγμα : Να βρεθεί ο Μ.Κ. Δ. των αριθμών 6, 18, 36
Δ18 : 1, 2, 3, 6, 9,18 Δ24 : 1, 2, 3, 6, 8, 12, 24 Δ28 : 1, 2, 4, 7, 14, 28 Κοινοί διαιρέτες : 1, 2
Μ.Κ.Δ.6, 12, 36 : 2
B΄ τρόπος
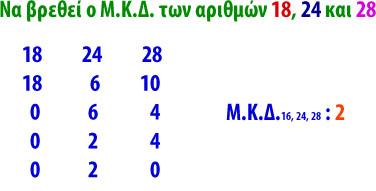
Γράφουμε στη σειρά τους αριθμούς.
Στη δεύτερη σειρά γράφουμε το μικρότερο και διαιρούμε μ αυτόν τους άλλους δύο, γράφοντας κάτω από τον καθένα το υπόλοιπο της διαίρεσης.
Στην επόμενη σειρά γράφουμε πάλι το μικρότερο (εκτός από το 0, αν υπάρχει) και κάνουμε το ίδιο με πριν.
Όταν απομείνει μόνο ένας αριθμός (εκτός από το 0), αυτός θα είναι και ο Μ.Κ.Δ. των αριθμών που είχαμε.
Γ΄ τρόπος
Γράφουμε στη σειρά τους αριθμούς και δεξιά του τελευταίου χαράσσουμε μια κάθετη γραμμή.
Δεξιά της γραμμής γράφουμε τον μικρότερο αριθμό (εκτός από το 1) που διαιρεί όλους μας τους αριθμούς.
Στην επόμενη γραμμή κάτω από κάθε αριθμό γράφουμε το πηλίκο της διαίρεσης.
Συνεχίζουμε την ίδια διαδικασία μέχρι να μην υπάρχει αριθμός που να τους διαιρεί όλους.
Πολλαπλασιάζουμε μεταξύ τους τους αριθμούς που γράψαμε δεξιά της γραμμής και το γινόμενο είναι ο Μ.Κ.Δ. των αριθμών που είχαμε.
