Σύστημα αρίθμησης
Πρόσθεση και Αφαίρεση
Πολλαπλασιασμός
 Όταν έχουμε να κάνουμε πολλαπλασιασμό, προσέχουμε να γράψουμε επάνω τον μεγαλύτερο (πολλαπλασιαστέο) και κάτω τον μικρότερο αριθμό (πολλαπλασιαστή) και απλά να κάνουμε την πράξη. Κάθε φορά που αλλάζουμε ψηφίο στον πολλαπλασιαστή, ξεκινάμε το μερικό γινόμενο με 0. Στο τέλος, κάνω την πρόσθεση των μερικών γινομένων και ο πολ/σμος είναι έτοιμος.
Όταν έχουμε να κάνουμε πολλαπλασιασμό, προσέχουμε να γράψουμε επάνω τον μεγαλύτερο (πολλαπλασιαστέο) και κάτω τον μικρότερο αριθμό (πολλαπλασιαστή) και απλά να κάνουμε την πράξη. Κάθε φορά που αλλάζουμε ψηφίο στον πολλαπλασιαστή, ξεκινάμε το μερικό γινόμενο με 0. Στο τέλος, κάνω την πρόσθεση των μερικών γινομένων και ο πολ/σμος είναι έτοιμος.
Διαίρεση
 Για να κάνουμε τη διαίρεση, θα πρέπει να ξέρουμε πολύ καλά την προπαίδεια. Αν ξέρουμε την προπαίδεια μπορούμε να βρίσκουμε κάθε φορά πόσες φορές χωράει ο διαιρέτης στον διαιρετέο, που είναι και το πιο δύσκολο σημείο της. Από εκεί και μετά είναι εύκολο να κάνουμε τους πολλαπλασιασμούς και τις αφαιρέσεις.
Για να κάνουμε τη διαίρεση, θα πρέπει να ξέρουμε πολύ καλά την προπαίδεια. Αν ξέρουμε την προπαίδεια μπορούμε να βρίσκουμε κάθε φορά πόσες φορές χωράει ο διαιρέτης στον διαιρετέο, που είναι και το πιο δύσκολο σημείο της. Από εκεί και μετά είναι εύκολο να κάνουμε τους πολλαπλασιασμούς και τις αφαιρέσεις.
Κλάσματα
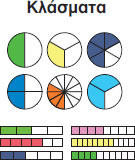 Κλάσματα είναι οι αριθμοί που αποτελούνται από μια οριζόντια γραμμή (κλασματική γραμμή), έναν αριθμό πάνω (αριθμητής) κι έναν αριθμό κάτω (παρονομαστής). Ο παρονομαστής δείχνει σε πόσα ίσα μέρη χωρίσαμε το ολόκληρο και ο αριθμητής πόσα ίσα μέρη πήραμε. Π.χ. το κλάσμα $\frac{3}{4}$ ενός πορτοκαλιού σημαίνει ότι κόψαμε το πορτοκάλι σε 4 ίσα μέρη και πήραμε τα 3.
Κλάσματα είναι οι αριθμοί που αποτελούνται από μια οριζόντια γραμμή (κλασματική γραμμή), έναν αριθμό πάνω (αριθμητής) κι έναν αριθμό κάτω (παρονομαστής). Ο παρονομαστής δείχνει σε πόσα ίσα μέρη χωρίσαμε το ολόκληρο και ο αριθμητής πόσα ίσα μέρη πήραμε. Π.χ. το κλάσμα $\frac{3}{4}$ ενός πορτοκαλιού σημαίνει ότι κόψαμε το πορτοκάλι σε 4 ίσα μέρη και πήραμε τα 3.
Δεκαδικοί αριθμοί
![]() Δεκαδικοί λέγονται οι αριθμοί που αποτελούνται (από αριστερά ξεκινώντας) από ακέραιο μέρος, την υποδιαστολή (,) και δεκαδικό μέρος. Το δεκαδικό μέρος δείχνει τι μέρος μιας ακέραιης μονάδας έχουμε πάρει. Αν έχουμε π.χ. τον δεκαδικό 3,78 διαβάζουμε τρία και 78 εκατοστά ή 3 ακέραιος και 78 εκατοστά ή 3 κόμμα 78.
Δεκαδικοί λέγονται οι αριθμοί που αποτελούνται (από αριστερά ξεκινώντας) από ακέραιο μέρος, την υποδιαστολή (,) και δεκαδικό μέρος. Το δεκαδικό μέρος δείχνει τι μέρος μιας ακέραιης μονάδας έχουμε πάρει. Αν έχουμε π.χ. τον δεκαδικό 3,78 διαβάζουμε τρία και 78 εκατοστά ή 3 ακέραιος και 78 εκατοστά ή 3 κόμμα 78.
Πράξεις με δεκαδικούς αριθμούς
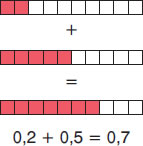 Για να κάνουμε προσθέσεις και αφαιρέσεις δεκαδικών θα πρέπει οι δεκαδικοί που χρησιμοποιούμε να έχουν τον ίδιο αριθμό δεκαδικών ψηφίων. Αν ένας δεκαδικός έχει 1 δεκαδικό ψηφίο και ο άλλος τρία, θα πρέπει στον πρώτο να συμπληρώσουμε τις τρεις θέσεις με 2 μηδενικά. π.χ. 3,6 + 2,345 → 3, 600 + 2, 345 ή 3,6 - 2,345 → 3, 600 - 2, 345
Για να κάνουμε προσθέσεις και αφαιρέσεις δεκαδικών θα πρέπει οι δεκαδικοί που χρησιμοποιούμε να έχουν τον ίδιο αριθμό δεκαδικών ψηφίων. Αν ένας δεκαδικός έχει 1 δεκαδικό ψηφίο και ο άλλος τρία, θα πρέπει στον πρώτο να συμπληρώσουμε τις τρεις θέσεις με 2 μηδενικά. π.χ. 3,6 + 2,345 → 3, 600 + 2, 345 ή 3,6 - 2,345 → 3, 600 - 2, 345
{
Συμμιγείς αριθμοί
Αριθμογραμμή
 Για να τοποθετήσουμε έναν αριθμό σε αριθμογραμμή θα πρέπει να ξέρουμε την αρχή και το τέλος της. Π.χ. στην αριθμογραμμή του βιβλίου αρχή είναι το 0 και τέλος το 1000. Με τα σημάδια που υπάρχουν πάνω στην αριθμογραμμή σχηματίζονται 10 διαστήματα. 1000 : 10 = 100 Άρα, το κάθε σημαδάκι διαφέρει από το διπλανό του κατά 100. Το πρώτο είναι το 100, το δεύτερο το 200, το τρίτο το 300 κ.λπ.
Για να τοποθετήσουμε έναν αριθμό σε αριθμογραμμή θα πρέπει να ξέρουμε την αρχή και το τέλος της. Π.χ. στην αριθμογραμμή του βιβλίου αρχή είναι το 0 και τέλος το 1000. Με τα σημάδια που υπάρχουν πάνω στην αριθμογραμμή σχηματίζονται 10 διαστήματα. 1000 : 10 = 100 Άρα, το κάθε σημαδάκι διαφέρει από το διπλανό του κατά 100. Το πρώτο είναι το 100, το δεύτερο το 200, το τρίτο το 300 κ.λπ.
 |
 |





