|
 |
 |
 |
 |
 |
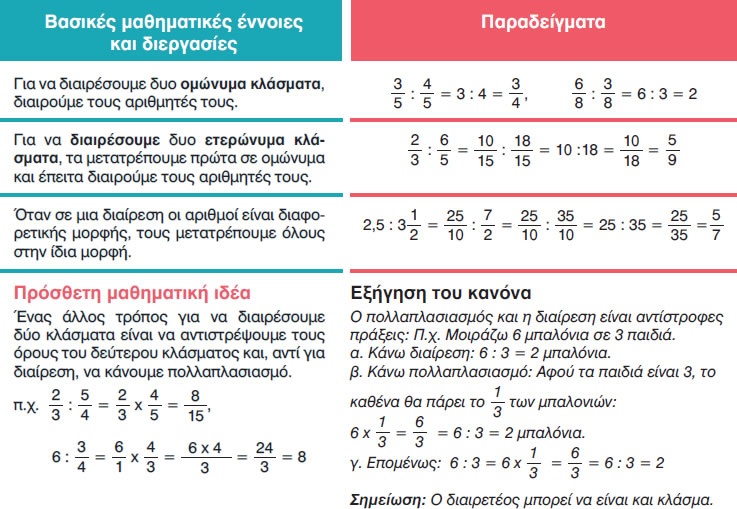
Πώς διαιρούμε ομώνυμα ή ετερώνυμα κλάσματα ;
Για να διαιρέσουμε ομώνυμα κλάσματα παίρνουμε τον αριθμητή του πρώτου κλάσματος και τον βάζουμε αριθμητή και τον αριθμητή του δεύτερου κλάσματος τον βάζουμε παρονομαστή.
$\frac{7}{8}$ : $\frac{3}{8}$ = 7 : 3 = $\frac{7}{3}$
$\frac{3}{5}$ : $\frac{4}{5}$ = 3 : 4 = $\frac{3}{4}$
Αν τα κλάσματα είναι ετερώνυμα, τα μετατρέπουμε σε ομώνυμα και στη συνέχεια κάνουμε τη διαίρεση.
$\frac{7}{8}$ : $\frac{3}{5}$ = $\frac{7×5}{8×5}$ : $\frac{3×8}{5×8}$ = $\frac{35}{40}$ : $\frac{24}{40}$ = 35 : 24 = $\frac{35}{24}$
$\frac{5}{6}$ : $\frac{1}{8}$ = $\frac{5× 8}{6× 8}$ : $\frac{1×6}{8×6}$ = $\frac{40}{48}$ : $\frac{6}{48}$ = 40 : 6 = $\frac{40}{6}$
Αν στη διαίρεση έχουμε διαφορετικά είδη αριθμών, τους μετατρέπουμε όλους στην ίδια μορφή και μετά ξεκινάμε τη διαίρεση.
Πώς διαιρούμε κλάσματα ;
Για να διαιρέσουμε 2 κλάσματα αντιστρέφουμε τους όρους του δεύτερου κλάσματος και αντί για διαίρεση κάνουμε πολλαπλασιασμό.
$\frac{3}{5}$ : $\frac{4}{7}$ = $\frac{3}{5}$ × $\frac{7}{4}$ = $\frac{3×7}{5×4}$ = $\frac{21}{20}$
$\frac{2}{9}$ : $\frac{1}{9}$ = $\frac{2}{9}$ × $\frac{9}{1}$ = $\frac{2×9}{9×1}$ = $\frac{18}{9}$ = 2
 |
 |