|
 |
 |
 |
Λύση προβλήματος (1)
ΠΡΟΒΛΗΜΑ
Ένα πενταμελές συνεργείο ολοκληρώνει το βάψιμο ενός κτιρίου σε 12 ημέρες. Σε πόσες ημέρες θα ολοκληρωθεί ο χρωματισμός ενός ίδιου κτιρίου αν το συνεργείο γινόταν 6μελές ;
1. Κάνουμε τον πίνακα ποσών και τιμών :
| ΠΟΣΑ | ΤΙΜΕΣ | |
| Εργάτες | 5 | 6 |
| Ημέρες | 12 | Χ |
2. Συγκρίνουμε τα ποσά :
Αν διπλασιάσουμε τους εργάτες, οι μέρες θα μειωθούν στο μισό. Άρα τα ποσά είναι αντιστρόφως ανάλογα. Άρα θα λύσουμε με γινόμενα αντίστοιχων τιμών.
3. Λύση
|
6*Χ = 5 * 12 6Χ = 60 Χ = 60 : 6 Χ= 10 |
4α. Λογικός Έλεγχος : Αφού αυξήθηκαν οι εργάτες οι μέρες θα έπρεπε να είναι λιγότερες. Όντως με έναν εργάτη παραπάνω (6), οι μέρες μειώθηκαν (10).
4β. Απάντηση : Αν το συνεργείο γίνει 6μελές θα χρειαστούν 10 ημέρες για την ολοκλήρωση του χρωματισμού του κτιρίου.
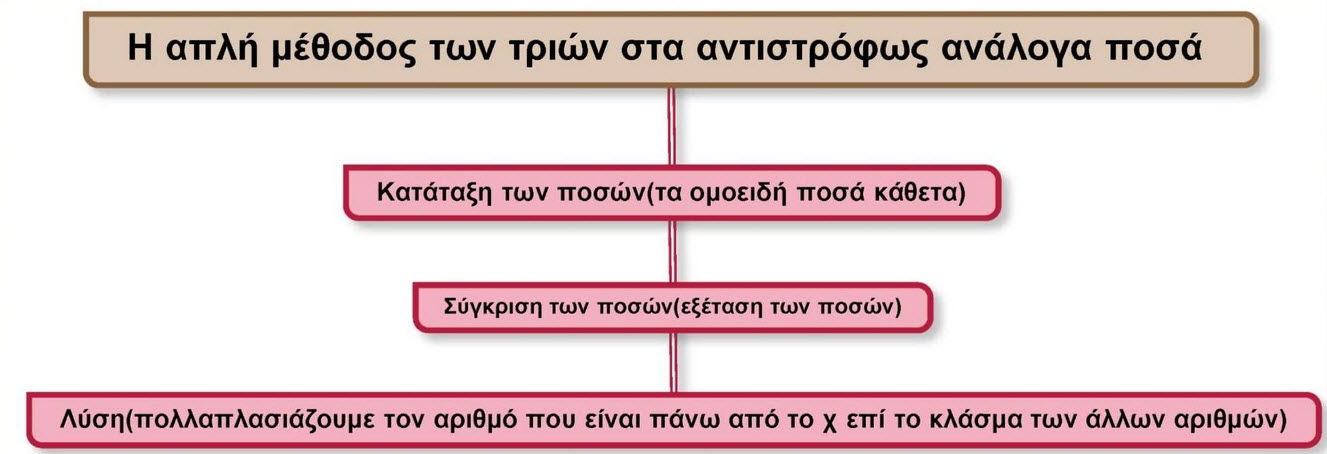
Το ίδιο πρόβλημα θα μπορούσαμε να το λύσουμε με Απλή Μέθοδο των Τριών :
1.Κατάταξη :
| Οι 5 εργάτες | ολοκληρώνουν το έργο σε | 12 ημέρες |
| Οι 6 εργάτες | >> | Χ ημέρες |
| ------------------------------------------------------------------------ | ||
2. Συγκρίνουμε τα ποσά :
Αν διπλασιάσουμε τους εργάτες, οι μέρες θα μειωθούν στο μισό. Άρα τα ποσά είναι αντιστρόφως ανάλογα.
3. Λύση
4α.Λογικός Έλεγχος : Αφού αυξήθηκαν οι εργάτες, οι μέρες θα πρέπει να είναι λιγότερες. Όντως με έναν εργάτη παραπάνω (6), οι μέρες μειώθηκαν (10).
4β. Απάντηση : Αν το συνεργείο γίνει 6μελές θα χρειαστούν 10 ημέρες για την ολοκλήρωση του χρωματισμού του κτιρίου.
Άρα :
Για να λύσουμε ένα πρόβλημα αντίστροφων ποσών με Απλή Μέθοδο των Τριών, πολλαπλασιάζουμε τον αριθμό που είναι στην κατάταξη πάνω από το Χ με το κλάσμα που δημιουργούν οι τιμές του άλλου ποσού.
Λύση προβλήματος (2)
Πρόβλημα
Σ' ένα στρατιωτικό φυλάκιο είναι 14 στρατιώτες και έχουν τροφή για 10 ημέρες. Για πόσες ημέρες θα φτάσει η τροφή αν οι στρατιώτες γίνουν 20 ;
1. Κατάταξη
| 14 στρατιώτες | έχουν τροφή για | 10 ημέρες |
| 20 στρατιώτες | >> | Χ ημέρες |
| ------------------------------------------------------------------ |
||
2. Συγκρίνουμε τα ποσά :
Αν διπλασιάσουμε τους στρατιώτες, η τροφή θα είναι επαρκής για τις μισές ημέρες. Άρα τα ποσά είναι αντιστρόφως ανάλογα.
3. Λύση
$$x = 10 ·\frac{14}{20}= \frac{140}{20} = 7$$
4α. Λογικός Έλεγχος : Αφού αυξήθηκαν οι στρατιώτες οι μέρες θα έπρεπε να είναι λιγότερες. Πράγματι με 6 στρατιώτες παραπάνω (20), οι μέρες για τις οποίες θα επαρκέσει η τροφή μειώθηκαν (7).
4β. Απάντηση : Αν οι στρατιώτες στο φυλάκιο γίνουν 20, η τροφή θα επαρκέσει για 7 ημέρες.