01.16 Πολλαπλάσια ενός αριθμού

Ορισμοί : Πολλαπλάσια - Κοινά Πολλαπλάσια - Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.)

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (1)

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (2)

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (3)

Ένας άλλος τρόπος για να βρούμε το Ε.Κ.Π. δύο ή περισσοτέρων αριθμών είναι να τους διαιρούμε με τον μικρότερο πρώτο αριθμό που διαιρεί έστω έναν από αυτούς. Όσοι δε διαιρούνται γράφονται από κάτω όπως και το πηλίκο αυτών που διαιρούνται. Στη συνέχεια διαιρούμε είτε με τον ίδιο αριθμό, αν διαιρεί έστω έναν από τους αριθμούς που έχουμε είτε με τον επόμενο πρώτο αριθμό. Η διαδικασία συνεχίζεται μέχρι τα αποτελέσματα κάτω από κάθε αριθμό να είναι 1. Πολλαπλασιάζουμε τους πρώτους αριθμούς με τους οποίους κάναμε τις διαιρέσεις και το γινόμενό τους είναι το Ε.Κ.Π.

Π.χ. Να βρεθεί το Ε.Κ.Π.(12, 15, 18)

Ξεκινάμε να διαιρούμε με το 2, επειδή υπάρχουν αριθμοί, οι οποίοι διαιρούνται με αυτό. Κάτω από τον καθένα γράφουμε το πηλίκο της διαίρεσής του με το 2, ενώ κάτω από το 15 που δε διαιρείται με το 2 γράφουμε πάλι 15. Τώρα έχουμε τους αριθμούς 6, 15 και 9.

Υπάρχει αριθμός (το 6) που διαιρείται με το 2, οπότε το ξαναγράφουμε δεξιά της κάθετης και διαιρούμε το 6, ενώ κατεβάζουμε το 15 και το 9. Τώρα έχουμε τους αριθμούς 3, 15 και 9.

Το 2 δεν διαιρεί πλέον κανέναν αριθμό. Επιλέγουμε τον επόμενο πρώτο αριθμό, δηλαδή το 3.

Το 3 διαιρεί το 3, το 15 και το 9. Γράφουμε από κάτω τα πηλίκα και συνεχίζουμε με το 3. Τώρα έχουμε τους αριθμούς 1, 5 και 1. Επιλέγουμε τώρα το 5. Όλα τα πηλίκα θα γίνουν 1.

Ε.Κ.Π._{(12, 15, 18)} = 2 * 2 * 3 * 5 = 2² * 3 * 5 = 180

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (4)

Ο τελευταίος τρόπος για να βρούμε το Ε.Κ.Π. έχει να κάνει με τα δεντροδιαγράμματα. Αναλύουμε καθέναν από τους αριθμούς, των οποίων θέλουμε να βρούμε το Ε.Κ.Π. Γράφουμε το γινόμενο των πρώτων αριθμών στους οποίους αναλύεται ο πρώτος από αυτούς. Σ' αυτούς πολλαπλασιάζουμε τους πρώτους αριθμούς στους οποίους πολλαπλασιάζεται ο δεύτερος. Δε γράφουμε τους πρώτους αριθμούς που έχουμε ήδη γράψει. Με τον ίδιο τρόπο συνεχίζουμε για τον επόμενο αριθμό. Κάνουμε τις πράξεις και το αποτέλεσμα είναι το Ε.Κ.Π. των αριθμών.

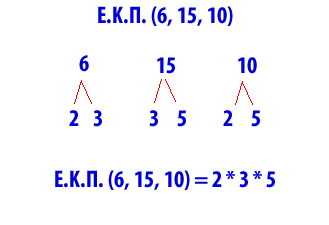
Π.χ. Να βρεθεί το Ε.Κ.Π._{(6, 15, 10)}

Αναλύουμε το 6, το 15 και το 10 σε γινόμενα πρώτων παραγόντων. ΕΚΠ είναι το γινόμενο των κοινών και μη κοινών πρώτων παραγόντων.

Γράφουμε το γινόμενο 2 * 3 που είναι οι πρώτοι παράγοντες στους οποίους αναλύεται το 6. Πάμε να γράψουμε αμέσως μετά τους πρώτους παράγοντες στους οποίους αναλύεται το 15, δηλαδή το 3 και το 5. Το 3 επειδή ήδη το έχουμε γράψει, δεν το ξαναγράφουμε και γράφουμε μόνο το 5. Πάμε να γράψουμε αμέσως μετά τους πρώτους παράγοντες στους οποίους αναλύεται το 10, δηλαδή το 2 και το 5. Και οι δύο παράγοντες έχουν ήδη γραφεί, οπότε δεν τους ξαναγράφουμε. Εδώ τελειώσαμε. Ε.Κ.Π.(6, 15, 10) = 2 * 3 * 5 =30

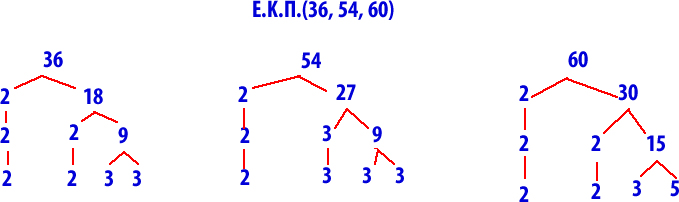
Να βρεθεί το Ε.Κ.Π._{(36, 54, 60)}

Το 36 αναλύεται : 36 = 2² * 3²

Το 54 αναλύεται : 54 = 2 * 3³

Το 60 αναλύεται : 60 = 2²*3*5

Κοινοί παράγοντες είναι το 2 και το 3. Θα τους πάρουμε μία φορά αλλά με τον μεγαλύτερο εκθέτη 2²και 3³ . Στο γινόμενο αυτών των αριθμών θα πολλαπλασιάσω και το 5 που είναι μη κοινός παράγοντας (επειδή υπάρχει μόνο σε έναν από τους τρεις αριθμούς). Άρα Ε.Κ.Π._{(36, 54, 60)} = 2²* 3³* 5 = 540

Άμεσος Υπολογισμός του Ε.Κ.Π. τριών αριθμών (κλικ)

paixnidia quiz

01.16 Πολλαπλάσια ενός αριθμού - Ε.Κ.Π.

Ορισμοί : Πολλαπλάσια - Κοινά Πολλαπλάσια - Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.)

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (1)

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (2)

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (3)

Bρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών (4)