 |
 |
 |
 |
 |
 |
Η διαίρεση και η ορολογία της
Διαίρεση λέγεται η πράξη με την οποία μοιράζουμε έναν αριθμό σε τόσα ίσα μέρη, όσα μας λέει ένας άλλος αριθμός.
Έχουμε δυο ειδών διαιρέσεις :
α) Τη διαίρεση μερισμού. Όταν ξέρουμε την τιμή των πολλών μονάδων και ζητάμε την τιμή της μιας μονάδας. Π.χ. Οι πέντε σοκολάτες κοστίζουν 7,5 €. Πόσο κοστίζει η μία ;
β) Τη διαίρεση μέτρησης. Όταν ξέρουμε και την τιμή των πολλών μονάδων και την τιμή της μιας μονάδας και δεν ξέρουμε πόσες είναι αυτές οι πολλές μονάδες. Π.χ. Αν έχω 12 κιλά μέλι και γεμίσω βάζα των 2 κιλών το καθένα. Πόσα βάζα χρησιμοποίησα;
- Ο αριθμός που μοιράζουμε σε ίσα μέρη λέγεται διαιρετέος. Ο αριθμός που μας δείχνει σε πόσα μέρη θα μοιράσουμε τον διαιρετέο λέγεται διαιρέτης.
- Ο αριθμός που βρίσκουμε από τη διαίρεση λέγεται πηλίκο και αυτός που τυχόν περισσεύει λέγεται υπόλοιπο.
- Το πηλίκο φανερώνει πόσες φορές χωρά ο διαιρέτης στον διαιρετέο.
- Όταν η διαίρεση αφήνει υπόλοιπο, λέγεται ατελής, αντίθετα όταν δεν αφήνει, λέγεται τέλεια.
Ιδιότητες της διαίρεσης
Να έχω υπόψη μου ότι :
- Αν πολλαπλασιάσω τον διαιρέτη (δ) με το πηλίκο (π) και προσθέσω και το υπόλοιπο (υ) (αν υπάρχει), αυτό που θα βρώ θα είναι ο διαιρετέος (Δ). Αυτή είναι και η δοκιμή της διαίρεσης. Δ = δ × π + υ
- Στη διαίρεση δεν ισχύει η αντιμεταθετική ιδιότητα.
- Η διαίρεση και ο πολλαπλασιασμός είναι αντίστροφες πράξεις.
Να μην ξεχάσω :
- Η διαίρεση ενός αριθμού με τον εαυτό του δίνει πηλίκο 1. π.χ. 5 : 5 = 1
- Η διαίρεση του μηδενός με έναν αριθμό δίνει πηλίκο 0 . π.χ. 0 : 2 = 0
- Διαίρεση με διαιρέτη το 0 δε γίνεται.
- Η διαίρεση ενός αριθμού με το 1 δίνει πηλίκο τον ίδιο τον αριθμό. π.χ. 5 : 1 = 5
- Αν πολλαπλασιάσουμε ή διαιρέσουμε και τον διαιρετέο και τον διαιρέτη με τον ίδιο αριθμό το πηλίκο παραμένει το ίδιο.
Παράδειγμα : 20 : 4 = 5
Πολλαπλασιάζω και τον διαιρετέο και τον διαιρέτη με τον ίδιο αριθμό π.χ. με το 2 :
20 Χ 2 = 40 4 Χ 2 = 8 Πολλαπλασιάζω τώρα τα αποτελέσματα που πήρα : 20 : 8 = 5 Το αποτέλεσμα παραμένει το ίδιο.
20 : 2 = 10 4 : 2 = 2 Διαιρώ τώρα τα αποτελέσματα που πήρα : 10 : 2 = 5 Το αποτέλεσμα παραμένει το ίδιο.
Παράδειγμα τέλειας διαίρεσης
Αν ένα ποδήλατο κοστίζει 125 €, πόσα τέτοια ποδήλατα μπορούμε να αγοράσουμε με 3.500 € ;
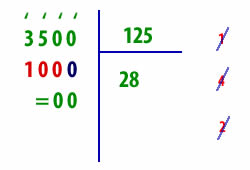 Τρία ψηφία έχει ο διαιρέτης, τρία χωρίζουμε και από την αρχή του διαιρετέου ή από τα αριστερά του διαιρετέου (τονίζουμε το 3, το 5 και το 0). Το 125 στο 350 χωράει 2 φορές. Γράφουμε το 2 κάτω από τον διαιρέτη. Αυτό το πολλαπλασιάζουμε μετά με τα ψηφία του διαιρέτη, πρώτα με τις μονάδες μετά με τις δεκάδες του και μετά με τις εκατοντάδες, και λέμε: 2 φορές το 5, κάνει 10, από 0 (από το τελευταίο τονισμένο ψηφίο) δεν αφαιρείται. Δανειζόμαστε 1 δεκάδα και λέμε 10 από 10, μένει 0. Το γράφουμε κάτω από το 0 από το οποίο αφαιρέσαμε.
Τρία ψηφία έχει ο διαιρέτης, τρία χωρίζουμε και από την αρχή του διαιρετέου ή από τα αριστερά του διαιρετέου (τονίζουμε το 3, το 5 και το 0). Το 125 στο 350 χωράει 2 φορές. Γράφουμε το 2 κάτω από τον διαιρέτη. Αυτό το πολλαπλασιάζουμε μετά με τα ψηφία του διαιρέτη, πρώτα με τις μονάδες μετά με τις δεκάδες του και μετά με τις εκατοντάδες, και λέμε: 2 φορές το 5, κάνει 10, από 0 (από το τελευταίο τονισμένο ψηφίο) δεν αφαιρείται. Δανειζόμαστε 1 δεκάδα και λέμε 10 από 10, μένει 0. Το γράφουμε κάτω από το 0 από το οποίο αφαιρέσαμε.
Τις δανεικές δεκάδες που πήραμε τις γράφουμε δίπλα, για να μην τις ξεχάσουμε. Ύστερα λέμε: 2 φορές το 2, κάνει 4 και 1 το κρατούμενο (το διαγράφουμε) 5, από 5, μένουν 0. (Το γράφουμε από κάτω).
 Συνεχίζουμε και λέμε: 2 φορές το 1, κάνει 2, από 3, 1. (Τα γράφουμε από κάτω).Τονίζουμε ύστερα στον διαιρετέο το επόμενο ψηφίο (0) και το κατεβάζουμε δίπλα στο 100 και έτσι αυτό γίνεται 1000. Λέμε μετά: Το 125 στο 1000 χωράει 8 φορές. Γράφουμε το 8 στο πηλίκο και συνεχίζουμε όπως προηγουμένως :
Συνεχίζουμε και λέμε: 2 φορές το 1, κάνει 2, από 3, 1. (Τα γράφουμε από κάτω).Τονίζουμε ύστερα στον διαιρετέο το επόμενο ψηφίο (0) και το κατεβάζουμε δίπλα στο 100 και έτσι αυτό γίνεται 1000. Λέμε μετά: Το 125 στο 1000 χωράει 8 φορές. Γράφουμε το 8 στο πηλίκο και συνεχίζουμε όπως προηγουμένως :
8 φορές το 5 κάνει 40, από 0 (το πρώτο από δεξιά) δεν αφαιρείται. Δανειζόμαστε 4 δεκάδες και λέμε : 40 από 40, 0. Γράφουμε το 0 κάτω από το 0 από το οποίο αφαιρούσαμε.
8 φορές το 2, 16 και 4 τα κρατούμενα (σβήνουμε τα 4 κρατούμενα) 20 από 0 δεν αφαιρείται. Δανειζόμαστε 2 δεκάδες και λέμε 20 από 20, 0. Γράφουμε το 0 κάτω από το 0 από το οποίο αφαιρούσαμε.
8 φορές το 1, 8 και 2 τα κρατούμενα (σβήνουμε τα 2 κρατούμενα), 10 από 0 δεν αφαιρείται. Επειδή φτάσαμε στο τέλος των ψηφίων από τα οποία αφαιρούμε παίρνουμε και το 1 και λέμε 10 από 10, 0. Κάτω από το 0 γράφουμε = αυτή τη φορά, επειδή εδώ τελείωσε η διαίρεση.
Απάντηση : Με 3.500 € αγοράζουμε 28 ποδήλατα.
Στην ατελή διαίρεση η πράξη γίνεται όπως παραπάνω, μόνο που αντί για μηδέν υπάρχει υπόλοιπο. Μπορούμε να συνεχίσουμε μια ατελή διαίρεση μέχρι να βρούμε 0 στο υπόλοιπο ή σε όσα δεκαδικά ψηφία θέλουμε.
ΠΡΟΣΟΧΗ : Το υπόλοιπο της διάιρεσης ποτέ δεν πρέπει να είναι μεγαλύτερο από το διαιρέτη. Αν συμβεί αυτό, σημαίνει ότι έχουμε κάνει λάθος στις πράξεις.
Διαίρεση δεκαδικών
α) Διαίρεση δεκαδικού αριθμού με ακέραιο αριθμό
Παράδειγμα:
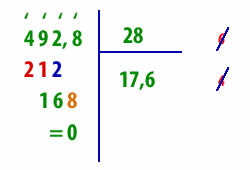 Πρόβλημα: Ενας γεωργός είχε να πουλήσει 492,8 κιλά λάδι. Για να το μεταφέρει, το έβαλε, εξίσου, σε 28 δοχεία και το μετέφερε στην αγορά. Πόσα κιλά λάδι έβαλε στο κάθε δοχείο;
Πρόβλημα: Ενας γεωργός είχε να πουλήσει 492,8 κιλά λάδι. Για να το μεταφέρει, το έβαλε, εξίσου, σε 28 δοχεία και το μετέφερε στην αγορά. Πόσα κιλά λάδι έβαλε στο κάθε δοχείο;
Απάντηση: Βρήκαμε ότι έβαλε στο κάθε δοχείο 17,6 κιλά λάδι. 
β) Διαίρεση ακέραιου αριθμού με δεκαδικό αριθμό
Για να διαιρέσουμε έναν ακέραιο αριθμό με δεκαδικό, σβήνουμε την υποδιαστολή από τον διαιρέτη, γιατί διαίρεση με δεκαδικό διαιρέτη δε γίνεται, και βάζουμε στο τέλος του διαιρετέου τόσα μηδενικά όσα δεκαδικά ψηφία έχει ο διαιρέτης, για να μην αλλάξει το πηλίκο. Έτσι, η διαίρεση στην περίπτωση αυτή γίνεται διαίρεση ακεραίου με ακέραιο.
Διευκρινίζουμε ότι σβήνοντας την υποδιαστολή από τον διαιρέτη, είναι σαν να πολλαπλασιάζεται με το 10,100 ή 1000, ανάλογα με το πόσα δεκαδικά ψηφία έχει. Για να μην αλλάξει το πηλίκο, πολλαπλασιάζουμε με τον ίδιο αριθμό, 10, 100 ή 1000 και τον διαιρετέο. Επειδή ο διαιρετέος είναι ακέραιος, ο πολλαπλασιασμός αυτός γίνεται με την προσθήκη ενός, δύο ή τριών μηδενικών, ανάλογα.
Παράδειγμα:
 Πρόβλημα: Η τιμή της βενζίνης σ' ένα πρατήριο ήταν 1,20 ευρώ το λίτρο. Ενας οδηγός πλήρωσε στο πρατήριο αυτό 45 ευρώ. Πόσα λίτρα βενζίνη έβαλε;
Πρόβλημα: Η τιμή της βενζίνης σ' ένα πρατήριο ήταν 1,20 ευρώ το λίτρο. Ενας οδηγός πλήρωσε στο πρατήριο αυτό 45 ευρώ. Πόσα λίτρα βενζίνη έβαλε;
γ) Διαίρεση δεκαδικού αριθμού με δεκαδικό
Για να διαιρέσουμε δεκαδικό με δεκαδικό, σβήνουμε την υποδιαστολή από τον διαιρέτη και μεταφέρουμε την υποδιαστολή στον διαιρετέο τόσες θέσεις προς τα δεξιά, όσα δεκαδικά ψηφία έχει ο διαιρέτης. Αν ο διαιρετέος έχει τόσα δεκαδικά ψηφία όσα και ο διαιρέτης, η υποδιαστολή μεταφέρεται στο τέλος του και έτσι σβήνει. Αν έχει λιγότερα, προσθέτουμε για τις θέσεις που λείπουν μηδενικά.
Παράδειγμα:
 Πρόβλημα: Για κάθε ανδρικό παντελόνι χρειάζονται 1,20 μέτρα ύφασμα. Πόσα
Πρόβλημα: Για κάθε ανδρικό παντελόνι χρειάζονται 1,20 μέτρα ύφασμα. Πόσα  παντελόνια θα ράψει μια βιοτεχνία με 145,20 μέτρα ύφασμα;
παντελόνια θα ράψει μια βιοτεχνία με 145,20 μέτρα ύφασμα;
Όπως βλέπουμε, σβήσαμε την υποδιαστολή από το διαιρέτη και έτσι πολλαπλασιάστηκε επί 100 και έγινε ακέραιος. Για να μην αλλάξει το πηλίκο, πολλαπλασιάσαμε και το διαιρετέο επί 100, μεταφέροντας την υποδιαστολή του δύο θέσεις προς τα δεξιά. Έτσι έγινε και αυτός ακέραιος και διαιρέσαμε μετά ακέραιο με ακέραιο.
Μπορεί όμως στον διαιρετέο να μείνει η υποδιαστολή, αν αυτός έχει περισσότερα δεκαδικά ψηφία από τον διαιρέτη όπως: π.χ. 28,485 : 6,4 ή 284,85 : 64.
Να μην ξεχάσω
- Η δοκιμή στη διαίρεση των δεκαδικών γίνεται όπως και στων ακεραίων.

- Αν η διαίρεση μας δεν είναι τέλεια, μπορούμε να προχωρούμε και να φτάνουμε μέχρι τα χιλιοστά. Το λάθος που παραμένει στο πηλίκο από εκεί και πέρα είναι ασήμαντο.
- Για να διαιρέσουμε έναν δεκαδικό αριθμό διά του 10, 100 ή 1000 μεταφέρουμε την υποδιαστολή του τόσες θέσεις προς τα αριστερά, όσα μηδενικά έχει το 10, το 100 ή το 1000.
Π.χ. 28,5 :10 = 2,85 56,4:100 = 0,564 45,6:1000 = 0,0456

